This article was originally written in Spanish. However, an automatically translated version can be found here.
A ready-to-print PDF version of this article is also available here.
A veces resulta interesante poner a prueba diferentes conceptos teóricos y algoritmos utilizados en diferentes ramas de las matemáticas, y comprobar su grado de correspondencia y precisión respecto a la realidad.
En este caso el objetivo del estudio fue analizar un algoritmo incluido dentro del espectro de la teoría de grafos, conocido como el Cartero Chino. Este algoritmo permite, definido en base a conceptos de la rama previamente mencionada, obtener un camino cerrado de longitud mínima que visite todas las aristas de un grafo dado al menos una vez. Para grafos ponderados (como el utilizado en este caso), la longitud es definida como la suma de los pesos de cada arista que forma parte del camino.
Para ello se ha modelado la red de líneas y paradas de Metro Madrid, intentando obtener un camino que permita recorrerla en el menor tiempo posible, considerando además que el recorrido debe comenzar y terminar en el mismo punto (es decir, en la misma parada) y pasar al menos una vez por todas las paradas.
Punto de partida
El punto de inicio sobre el que se comenzó a modelar el grafo fue el mapa más actualizado de la red de Metro Madrid al momento de realizar la prueba (actualizado a fecha de Febrero de 2020), que se muestra a continuación:
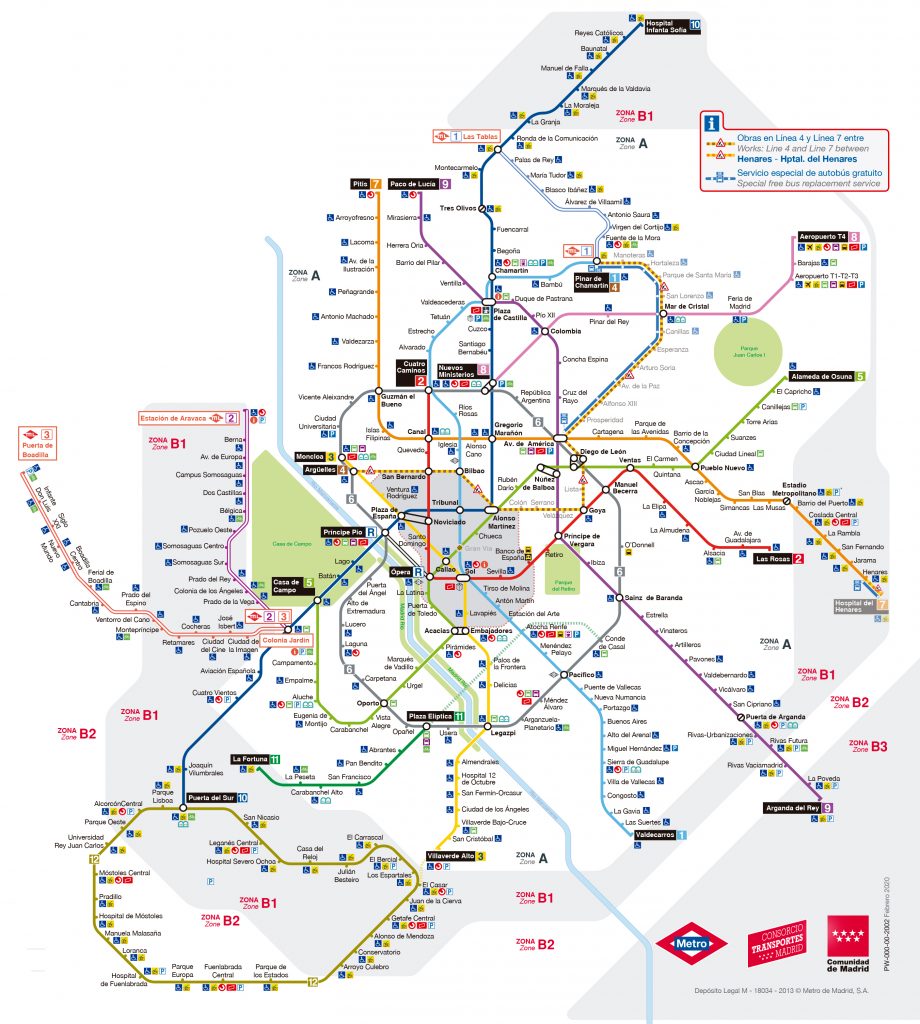
Características del grafo
En base a las características del problema a abordar, se han considerado las siguientes variables para el grafo utilizado:
- Vértices: aquellas paradas que permiten un transbordo entre varias líneas. Se han descartado aquellas que, aunque en el mapa original figuran como opción de transbordo, requieren atravesar un pasaje a pie de una longitud no despreciable.
- Aristas: trayecto de una o más líneas (mayoritariamente sólo una) entre dos estaciones.
- Ponderado: se define el peso de cada arista como el tiempo estimado que se tarda en recorrer el trayecto desde su vértice de origen a su vértice de destino[1].
- No dirigido: como las líneas de metro en cada parada permiten dirigirse hacia ambas direcciones, se han incluido las dos en una sola arista sin dirección definida.
Finalmente cabe remarcar que el grafo no contiene ningún bucle, ya que carece de sentido ir de una parada a sí misma, y tampoco contiene diferentes aristas entre un mismo par de vértices en aquellos casos en los que dicho trayecto se puede realizar en más de una línea, ya que se asume que el trayecto va a tener la misma duración independientemente de la línea en que se realice.
Herramientas utilizadas
Para la correcta realización del análisis y con el objetivo de acelerar tanto el modelado del grafo como la ejecución del algoritmo, el siguiente software y librerías fueron utilizadas:
- Adobe Photoshop CC, para trazar sobre el mapa de la red de Metro Madrid el primer boceto del grafo, remarcando las paradas y los trayectos convenientes y facilitar su posterior transformación al código.
- Librería JGraphT, basada en Java, que incluye las clases necesarias que implementan el tipo de grafo deseado, y permite ejecutar el algoritmo del Cartero Chino[2].
Obtención del grafo
En primer lugar, y antes de comenzar con cualquier otra fase, se comprobó el funcionamiento de las librerías elegidas, siguiendo ejemplos con resultados ya conocidos[3].
Una vez comprobado el adecuado funcionamiento de dichas librerías se comenzó con el modelado del grafo, marcando sobre el mapa previamente mostrado las paradas de interés y sus correspondientes trayectos. Finalizada esta etapa, el mapa/grafo se encontraba en el siguiente estado:
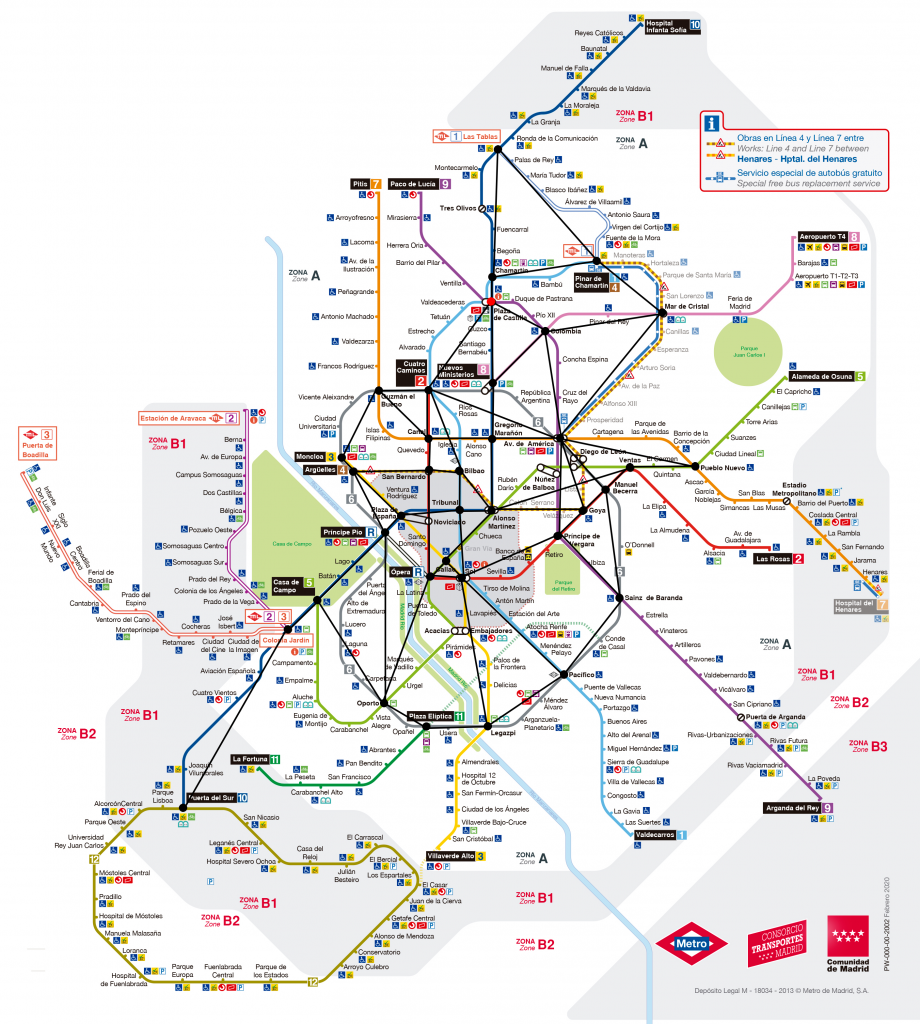
Como se puede observar, sobre la red original de paradas y líneas se encuentran marcadas con puntos negros aquellas paradas que incluyen transbordos entre varias líneas, y éstas se encuentran unidas entre sí en base a los trayectos que las unen pero dispuestas en línea recta, para facilitar la representación visual posterior del grafo final.
Se eliminaron del grafo los trayectos que no incluyen ningún transbordo y que representan el final de cada línea, ya que se conoce que la única manera de recorrerlos sería linealmente, en un trayecto de ida seguido del mismo trayecto de vuelta, sin ningún transbordo durante ese recorrido. De este modo, posteriormente se detalla que, una vez el camino alcanza uno de estos recorridos, se deben recorrer de la manera especificada, sin ser necesario que esto sea representado en el modelo.
Seguidamente, eliminando ya el fondo del mapa original, se añadieron etiquetas a los vértices (paradas) del grafo, representados por el nombre de cada una de las paradas, y también se rellenaron los pesos que corresponden a cada una de las aristas (trayectos), expresados en minutos de trayecto. De esta forma se asegura el parecido a la realidad, ya que los trayectos en Metro Ligero son más costosos debido a los vagones en los que se realizan, que viajan a una menor velocidad.
No se ha considerado en el cálculo del peso de las aristas el tiempo de espera a la llegada del tren ni el de transbordo (salir de un vagón de una línea y entrar a otro), ya que es un valor muy variable y que añadiría imprecisión al resultado final. Posteriormente, en la puesta en práctica de la ruta, se podría obtener una media del tiempo de espera debido a los factores mencionados.
Considerados todos los puntos anteriores, y realizadas las modificaciones especificadas, el grafo de 36 vertices y 64 aristas finalmente queda como se muestra a continuación:
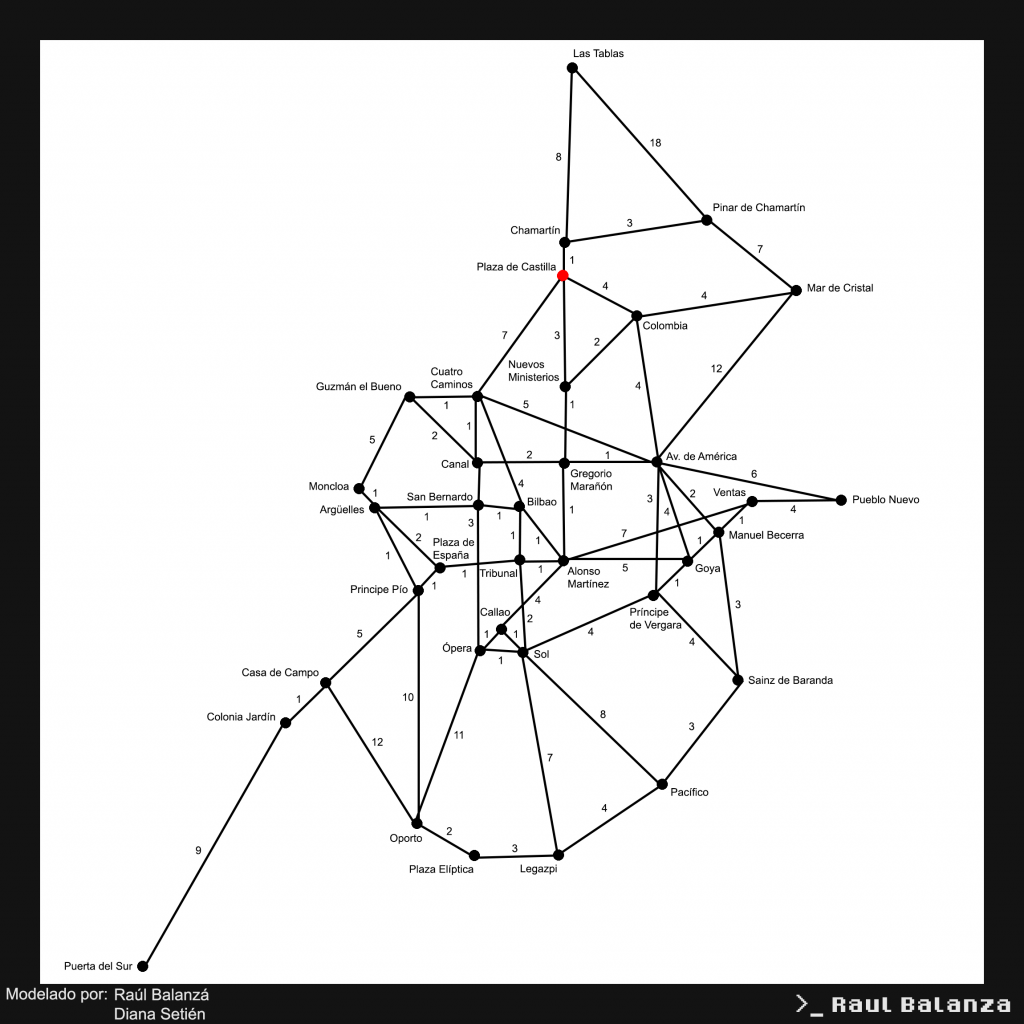
Ejecución del algoritmo
Una vez obtenido el grafo, se procedió a su adaptación a la sintaxis y la estructura impuesta por la librería JGraphT, elegida para la representación del grafo en código y la ejecución del algoritmo.
En este enlace se encuentra el código utilizado para la generación del grafo y para el cálculo del camino obtenido por el algoritmo del Cartero Chino. La lista de paradas y de trayectos considerada también está disponible.
La ejecución de el algoritmo siguiendo la implementación de la librería elegida tiene un coste temporal asintótico de O(N3), siendo N el número de vértices. Sin embargo, dado el tamaño del grafo obtenido, el tiempo de ejecución fue mínimo en este caso.
Al finalizar, se obtiene como resultado del cálculo la sucesión de transbordos a realizar, a partir de la cual se puede deducir el camino a seguir. También se puede estimar el coste total en tiempo de la realización del recorrido, definido como la suma de los pesos de todas las aristas que conforman el camino, y teniendo en cuenta las limitaciones previamente especificadas, es decir, sin tener en cuenta el tiempo de transbordo ni de espera al tren, y a falta de añadir el tiempo necesario para recorrer aquellos trayectos de ida y vuelta que representan los finales de línea y algunas líneas de Metro Ligero.
Trayectos lineales
Antes de detallar los resultados finales obtenidos tras la ejecución del algoritmo, conviene estimar el tiempo de duración de aquellos trayectos que no han sido considerados en el modelo original, para poder añadirlos a dicho análisis y obtener así una estimacion realista del tiempo requerido para recorrer toda la red de Metro Madrid.
Todos los trayectos se muestran con su tiempo duplicado, ya que se tiene en cuenta tanto el trayecto de ida como el de vuelta. Dichos trayectos son los que se listan a continuación, junto a su duración:
- Colonia Jardín <-> Puerta de Boadilla: 36 * 2 = 72 minutos.
- Colonia Jardín <-> Estación de Aravaca: 21 * 2 = 42 minutos.
- Plaza Elíptica <-> La Fortuna: 10 * 2 = 20 minutos.
- Legazpi <-> Villaverde Alto: 13 * 2 = 26 minutos.
- Pacífico <-> Valdecarros: 26 * 2 = 52 minutos.
- Sainz de Baranda <-> Arganda del Rey: 32 * 2 = 64 minutos.
- Ventas <-> Las Rosas: 9 * 2 = 18 minutos.
- Pueblo Nuevo <-> Hospital del Henares: 22 * 2 = 44 minutos.
- Pueblo Nuevo <-> Alameda de Osuna: 11 * 2 = 22 minutos.
- Mar de Cristal <-> Aeropuerto T4: 11 * 2 = 22 minutos.
- Las Tablas <-> Hospital Infanta Sofía: 17 * 2 = 34 minutos.
- Plaza de Castilla <-> Paco de Lucía: 10 * 2 = 20 minutos.
- Guzmán el Bueno <-> Pitis: 10 * 2 = 20 minutos.
- Puerta del Sur <-> Puerta del Sur (Línea 12 – circular): 32 minutos.
Todos los trayectos mencionados suman un total de 488 minutos adicionales (≈8.14 horas), un tiempo significativo a considerar.
Una vez más, cabe remarcar que sería necesario obtener una estimación media del tiempo de espera y de transbordo, que debería ser multiplicada por el número de transbordos realizados y sumada a los resultados que se exponen en la sección siguiente.
Resultados del análisis
Una vez consideradas todas las variables en el análisis, a continuación se presentan los datos obtenidos: el algoritmo del Cartero Chino obtuvo un camino eficiente para recorrer el núcleo de la red de Metro Madrid (la zona que abarca el grafo) en un tiempo aproximado de 273 minutos. Esta duración de trayecto se ve superada en gran magnitud por aquellas zonas que no pueden ser optimizadas, al solo disponer de una posibilidad de recorrido, añadiendo este factor un total de 488 minutos al recorrido previamente mencionado.
El total de tiempo en el que se podría recorrer, por tanto, la red de Metro Madrid, es de 761 minutos (unas 12.7 horas) + el tiempo necesario para esperar a los trenes y realizar transbordos. Obtenidos estos resultados, cabe destacar que sería técnicamente posible realizar este recorrido en un sólo dia de funcionamiento de la red, que está activa durante 20 horas al día, asumiendo que el tiempo de espera no supera en la mayoría de casos al de trayecto.
El camino requerido para poder obtener estos resultados se describe a continuación, a modo de lista de estaciones en las que realizar transbordo, situando el comienzo (y el final) de la ruta en la estación de Plaza de Castilla, y siempre considerando que se realizan las rutas lineales descritas previamente al llegar a su parada de comienzo:
[Plaza de Castilla, Cuatro Caminos, Guzman el Bueno, Moncloa, Arguelles, Principe Pio, Oporto, Plaza Eliptica, Legazpi, Pacifico, Sainz de Baranda, Manuel Becerra, Ventas, Pueblo Nuevo, Av. de America, Mar de Cristal, Colombia, Nuevos Ministerios, Gregorio Maranon, Alonso Martinez, Ventas, Manuel Becerra, Sainz de Baranda, Principe de Vergara, Sol, Pacifico, Legazpi, Sol, Opera, Oporto, Casa de Campo, Colonia Jardin, Puerta del Sur, Colonia Jardin, Casa de Campo, Principe Pio, Plaza de Espana, Tribunal, Sol, Callao, Sol, Tribunal, Alonso Martinez, Goya, Principe de Vergara, Av. de America, Manuel Becerra, Goya, Av. de America, Gregorio Maranon, Canal, San Bernardo, Bilbao, Alonso Martinez, Callao, Opera, San Bernardo, Arguelles, Plaza de Espana, Tribunal, Bilbao, Cuatro Caminos, Canal, Guzman el Bueno, Cuatro Caminos, Av. de America, Colombia, Nuevos Ministerios, Plaza de Castilla, Colombia, Mar de Cristal, Pinar de Chamartin, Chamartin, Pinar de Chamartin, Las Tablas, Chamartin, Plaza de Castilla]
Después de añadir al camino anterior las rutas lineales y de detallar los trayectos a seguir para llegar a los diferentes vértices del mismo, se obtiene la ruta completa a través de la red de Metro Madrid, que está disponible en este documento.
Conclusiones
Como punto final a este análisis, puede afirmarse que queda demostrada la (poca) viabilidad de realizar el recorrido de toda la red de Metro Madrid en el tiempo limitado de un día, incluso intentando maximizar su eficiencia.
Resulta llamativo observar la diferencia entre la duración del recorrido optimizado del núcleo de la red, que es prácticamente duplicada por la de una zona no optimizable, como es la periferia de la misma. Esto deja en evidencia la utilidad del algoritmo utilizado, y la importancia de hacer uso de herramientas como esta al realizar estimaciones de gran magnitud, lo cual era un objetivo principal del análisis expuesto en este artículo.
Sin embargo, independientemente de la utilidad práctica del análisis que aquí se expone, diferentes datos y mediciones pueden ser extraídos para otros propósitos. A modo de ejemplo, el grafo modelado de la red de Metro Madrid, con la adición de los trayectos lineales no incluidos, podría utilizarse junto a otros algoritmos como el algoritmo de Dijkstra, que permitiría obtener el camino más corto para realizar el trayecto desde una estación a otra, una aplicación muy útil y comunmente utilizada por los usuarios de transporte público.
Autores
- Raúl Balanzá: modelado del grafo, programación y redacción
- Diana Setién: modelado del grafo
Referencias
- [1]Citymapper: estimaciones de tiempo para todos los trayectos
- [2]JGraphT: librería programada en Java para uso de grafos
- [3]The Postman Problems, Universidad de La Laguna: ejemplos conocidos del algoritmo del Cartero Chino