This article was originally written in English. However, an automatically translated version can be found here.
The complete scientific paper with a detailed description of all the performed experiments and their solutions is available here.
In September of this year, I moved to Prague (Czech Republic 🇨🇿) to spend five months studying at the Czech Technical University in Prague (ČVUT) as part of an international exchange program during the last semester of my Bachelor’s degree.
For the semestral work of one of the courses that I am taking, I have had the opportunity of doing some research to compare several Artificial Intelligence approaches for the same purpose: recognizing and classifying handwritten digits.
The task of recognizing handwritten digits consists of observing an image of a written number and determining to which digit the image corresponds. This task, which is trivial for humans, has been deeply studied in the AI field, obtaining almost perfect results. However, the objective of this research was not (only) to find the most accurate approach to take: it was to find a balance between high accuracy and high ‘efficiency’ (i.e., a model that required the least amount of computing resources).
The dataset
MNIST, a very well-known dataset of computer vision, was the employed dataset for all the experiments that were carried out. This dataset has served since its release as the basis for benchmarking classification algorithms. It consists of a training set of 60K examples and a test set of 10K examples.
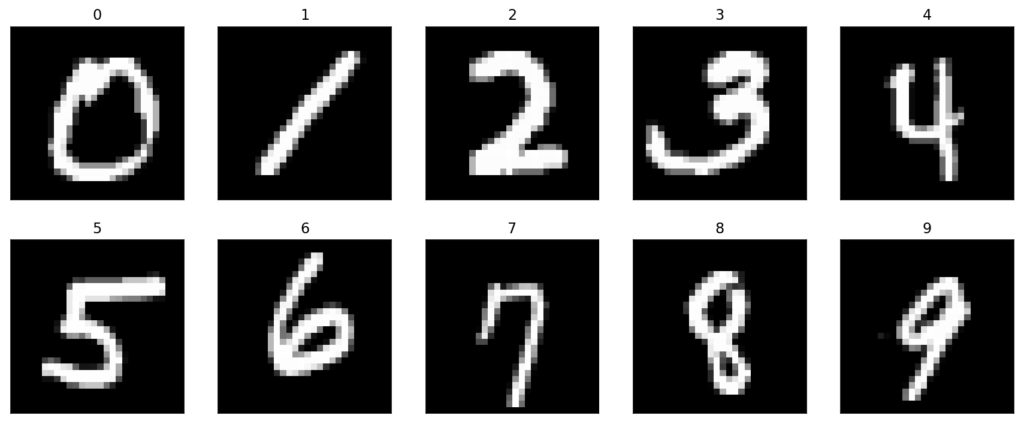
Although this dataset is effectively solved, it is still widely used for estimating the performance of some models, and deciding how to explore possible improvements. There also exist several variants of this dataset with different types of data, designed for similar purposes.
Experiments
During the whole research, a total of four computational intelligence techniques were used, with at least three variations for each of them in order to optimize as far as possible the accuracy of each model. A brief description of each of them follows.
Convolutional Neural Networks
CNNs are Deep Learning models that assign importance to various aspects of the input samples and are able to differentiate them from each other. The preprocessing required using this approach is much lower when compared to other classification algorithms, and the architecture is analogous to that of the connectivity pattern of neurons in the human brain.
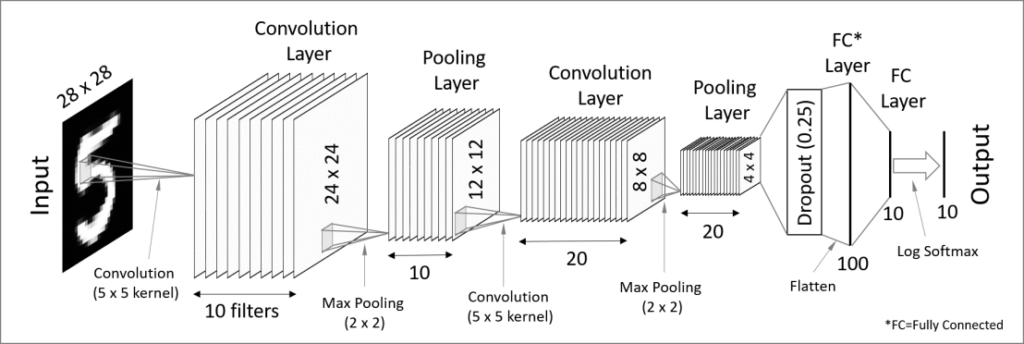
After designing a model and applying certain modifications to try to improve the final results, an accuracy of 98.85% was reached during training; and 99.31% during testing.
Zero-shot learning
ZSL is a problem setup in machine learning where, at test time, a learner observes samples from classes that were not observed during training, and needs to predict the class they belong to. These methods generally work by associating observed and non-observed classes through some form of auxiliary information, which encodes distinguishing properties of objects.
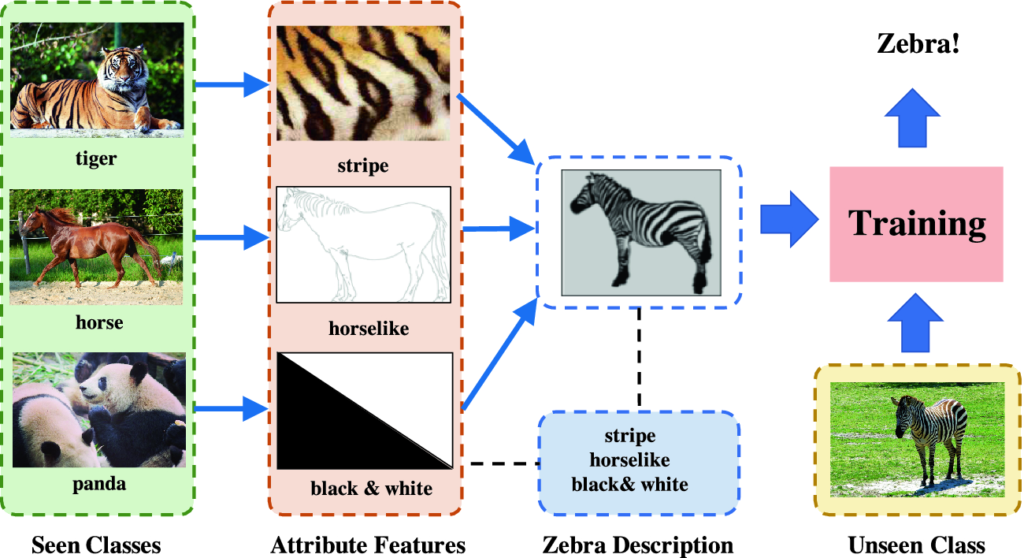
A model was designed in which some digits where provided in the training phase, and some only in the testing (inference) phase, an accuracy of 72.42% was reached during training; and 48.06% during testing.
However, it must be taken into account that this is a predictive approach with a limited amount of information in training time, an aspect that makes the results still considerably good.
k-Nearest Neighbors classifier
k-NN is a non-parametric classification method used for classification, among others. The input consists of the k closest training examples in a dataset, and the output is a class membership. An object is classified to the most common class among its nearest neighbors.
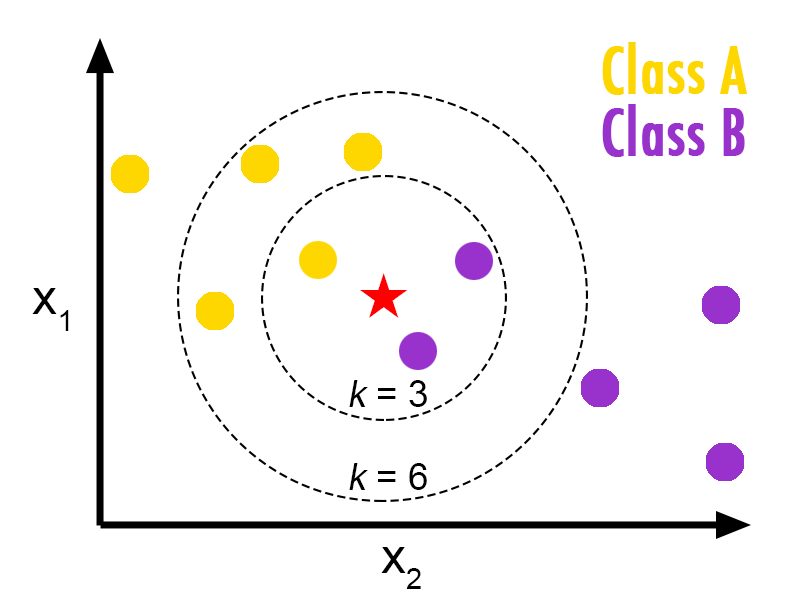
In this case, data was preprocessed using the PCA dimensionality reduction technique (to remove noisy data in each sample), and then classified using the k-NN method, using different values for k. An accuracy of 97.60% was reached during training; and 97.16% during testing.
Probability distributions
Finally, the last tested approach was to assume that the data followed different probability distributions, and to try estimating its parameters. In total, three distributions were explored.
Some smoothing techniques were applied on the data to avoid overfitting and, because each of these probability distributions are suitable for different kinds of data, it was required to preprocess the samples in some cases.
The results obtained for each of the distributions were:
- Bernoulli distribution: 83.47% training | 84.38% testing
- Multinomial distribution: 82.15% training | 83.67% testing
- Gaussian distribution: 95.73% training | 95.82% testing
Conclusions
After running all the experiments, several interesting results were obtained. As in can be seen, the digit recognition task still has many aspects to be explored in order to find the most optimal approach to take, finding a balance between accuracy and efficiency in terms of computing requirements.
The numbers show that the CNN model is the best performing one, followed closely by the k-NN approach. Considering the difficulty of training both approaches, and due to a very small difference in both results, the most efficient choice in this case would be to go for the second one.
Moreover, with respect to the probability distributions, several promising results were obtained for the Gaussian case, with an accuracy close to that of the previous two best approaches. However, the samples do not fit as well into the Bernoulli and Multinomial distributions.
Finally, the ZSL learning method obtained the worst results. Nevertheless, that model is, in fact, characterized for having the least amount of information input of all the considered approaches. It can be concluded that altough in MNIST the amount of classes is very well-defined, the results would be remarkable for an expandable class dataset with more dynamic information.